一次式であらわせる式でも、文章題などの応用問題では変域が存在する。 たとえば 窓があります。窓の高さは90 cmとします。窓を x cmあけたときの、あけられた部分の面積 y (単位はcm 2 とする)は、いくらでしょうか?基本上,「二元一次式」的觀念和「一元一次式」幾乎一樣, 差別只是式子的符號從 1 個變成 2 個而已,例如 2x 1 (一元,只有一個符號 x) 2x 3y 1 (二元,有兩個符號 x, y) 例:如图已知某一次函数的图像交X轴于点(1,0),交y轴于点(0,2),求这个一次函数的解析式。 解:首先设这个一次函数的解析式为y=kxb(k≠0), 把图像上的两点带入可得0=kb,2=0b 解得k=2,b=2 所以这个一次函数的解析式为y=2x2

分式型函数求值域最值
一次式的值与化简
一次式的值与化简-二次方程式に解を与える最初期の方法は幾何学的であった。バビロニアの楔形文字で書かれた文字板には二次方程式を解くことに単純化可能な問題が含まれていた エジプト中王国の時代(紀元前50年 紀元前1650年)にまで遡る、エジプトの ベルリンパピルス (英語版) には二項の二次方程式1次方程式 ⇒ 等式となる1次式。例えば「x1=0」 方程式の詳細は下記をご覧ください。 方程式とは?1分でわかる意味、移項、1次方程式の解き方と計算問題、分数の関係 1次式と2次式の違い 1次式と2次式の違いを下記に示します。 1次式 ⇒ 次数の最大値が1



化簡二元一次式 二元一次聯立方程式 發現學習的美麗新世界
一元一次方程式也被稱為线性 方程,因為在笛卡尔坐标系上任何一個一次方程的圖形都是一條直线。 组成一次方程的每一项必須是常数或者是一个常數和一个变量的乘積。 且方程中必須包含一个變量,因為如果没有變量只有常數,式子則是代数式而非方程式。 如果一次方程式中只包含一个文字符まとめ 整式を割った余りを求める問題は次のことがポイントとなります。 整式を1次式xαで割った余りはxαが0になる値x=αを代入して求める(剰余の定理)。 整式を2次以上の式で割った余りは,(余りの次数)<(割る式の次数)となるように余りをおいて,割り算について成り立つ等式をつくって一次因式提出公因式 在一个公式内把其公因子抽出, 一般 会得到,例子: 7 a 98 ab 其中,7 a 是公因子。 因此,提出公因式后得到的答案是:7 a (1 14 b ),这两个因式都是一次因式。 7a^214a^2 其中,7 a^2 是公因子。 因此,提出公因式后得到的答案是:7 a^2
通俗易懂竞赛保送生主讲干货满满数学有救了学高中数学有这个就够了!一数辞典合集 一数儿 11万 播放 35万 弹幕1次方程式か一次方程式か 新カリ用の教科書が次々,届いている.それらを見な がら,「あれ?」と思ったことがある. ある出版社の教科書で,数学i では「2 次関数」や「2 次不等式」と書きながら,数学a の教科書では「二元一 一次式の計算(分数)その1 次の計算をしましょう。 分数を含んだ一次式の和や差は、通分して求めます。 (1)であれば、 x− 2 x − 2 を、分母が 3 3 となるように変形してから次のように計算します。 2x −1 3 x−2 = 2x−1 3(x− 2) 3 = 2x −1 3x −6 3 = 5x −7 3
一次方程式は基本的にこの手順で全て解くことができます。 しかし、中には手順1に入る前の前段階ともいえる 手順0 を必要とする方程式もあります。 次では、そのような手順0を必要とする方程式を見ていきましょう。精選版 日本国語大辞典 一次式の用語解説 〘名〙 未知数の最高次数が一次の整式。 1次式(1次の項,\ 係数,\ 定数項1次の項だけ,\ または1次の項と定数項の和で表せる式 加法の記号${}$で結ばれた1つ1つの部分} {1次の項 & 文字が1つだけの項係数 & 文字を含む項の数の部分} $1次の項2}xの係数は\定数項 & 数だけの項} $1次式2x3}の定数項は\次の1次式の1次の項とその係数,\




一般 一元一次式 數字易位問題 Youtube




三角函数求最值的七种解法 个个实用 手慢无 知乎
二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解二元一次方程组的解:二元一次方程组的两个公共解,叫做二元一次方程组的解。 标准二元一次方程组包含六个系数,两个未知数,形式为: 式1,axby=c 式2,a2xb2y=c2不定積分の漸化式 → 携帯版は別頁 分数関数(有理関数)の不定積分 (例題中心) はじめに・目次 この頁で取り扱う不定積分 この頁では次の (1)~ (3), (A) (B)について解説と例を示す.実際の不定積分の計算においては (A) (B)を先に考えて, (1)~ (3)で 連続の式 管内の微小部分 を占める流体の質量は と表せて,同領域を占める質量の時間変化と,流入出量の等式を立てることが出来る.ただし, は壁面等から流入出がある場合の単位長さあたりの流入量を表す. この式から をはらってしまえば,一次元流れの連続の式が得られる




消元法解二元一次方程組的知識點與方法步驟 這些方法你掌握了嗎 每日頭條




中数学 解不等式的14种快速解题法 含经典题型 数学 Www Bifa7 Com
問 次の式はそれぞれ何次式かを答よ 3b / ab / b / 2a+5 / 9a+8b / 6a +4b+7 こんなの簡単じゃない。 要するに文字の数が次数なんでしょ? つまり 3b は「一次式」、ab と b は「二次式」だよね。 解析式法: 简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题中的函数关系,不能用解析式表示。 图象法: 形象直观,但只能近似地表达两个变量之间的函数关系。 (二)一次函数 Update 1、一次函数的定义 一般地,形如(k,b是常数,且k≠0)的函一元一次式的化簡 (舊教材) 代數式及其簡記 (舊教材) 一元一次式及其運算 ;




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




翻轉學習影片 國中 數學 4 1 1 二元一次式的意義 值與化簡
其中, 是二次项, 是一次项, 是常数项。 是一个重要条件,否则就不能保证该方程未知数的最高次数是二次。当然,在强调了是一元二次方程之后, 也可以省略不写。當然,一元二次方程式有時會出現虛數根。 歷史 古巴比伦留下的陶片显示,在大约公元前00年(00 BC)古巴比伦的数学家就能高校数学B 数列:漸化式17パターンの解法とその応用 漸化式 ( ぜんかしき )は、数列分野の最重要事項である。 大学受験という観点からすると、高校数学全体から見ても最重要事項の1つといえる。 要するに大学受験における出題頻度が極めて高い。 その动态32式 换姿势再来一次 男欢女爱动态截图百度 搞笑 动态32式 换姿势再来一次 男欢女爱动态截图百度 搞笑 ,欧美v高清资源不卡在线播放 mdash 免费播放观看在线视频 欧美v高清资源不卡在线播放 mdash 免费播放观看在线视频



名師課輔網 一次因式檢驗法




一元一次方程知識講解 經典例題講解 每日頭條
判别式一元二次方程判别式的应用 编辑 (1)解方程,判别一元二次方程根的情况. 它有两种不同层次的类型: ① 系数 都为数字; ②系数中含有字母; ③系数中的字母人为地给出了一定的条件. (2)根据一元二次方程根的情况,确定方程中字母的取值対応完了までの間、ご利用の際は恐れ入りますが、お使いの教科書等と照合して内容をご確認の上、用途に合わせてお使い頂きますようお願い致します。 21年4月9日 株式会社パディンハウス ツイート 中学1年生で習う簡単な一次式の乗法、除法、加法文字と式 目次 > はじめに、多項式の項と係数と次数について説明します。次に、これらの用語をもとに式の計算方法を説明します。多項式の用語 式 2x-5 を多項式といい、2x と-5 の2つの項からできています。 x の前の数 2 を係




分式型函数求值域最值




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
一次式 ax b を特徴付けるふたつの定数について、 a が増減すると対応する直線の「傾き」が急になったり緩やかになったりするので、 a はこの直線の傾きと呼ばれる。 また b は対応する直線と y軸との交点の座標であり y切片 (yintercept) あるいは単に切片と呼ばれる。違う種類の一次式がかけられたものと、同じ一次式が二乗されたものです。 次の例題で分解方法を確認してみましょう。 例題1 まずは公式\((1)\)を使った例です。例題として以下の式を部分分数分解してみたいと思います。 $$\frac{x2}{x(x1)}$$になります. 例10 右のような直線の方程式を読み取りたいとき, 青の点の y 座標から切片は −2 です. 次に,傾きを求めるときに, x が 1 だけ増加したときの y の増加を読み取ろうとすると,分数(小数)になってしまって正確に読み取れません. そこで,右に進んで x 座標, y 座標の両方




中1 一次式 項 係数 まとめ 中学生 数学のノート Clear



求三角函数最大最小值基本题型概括
一元一次式未知數的位置 一個一元一次式的未知數 不可以在 分母 ,但是 可以放在分子 。如: 不是一元一次式,但 是一元一次式。 不可以 有一個以上不同 的未知數。如: 不是一元一次式。 資料夾名稱 二元一次聯立方程式 (ch1) 發表人 顧震宇 單位 台灣數位學苑 (k12 數學) 建立 最近修訂エルミート多項式は次の直交性を満たす。 第一項は、指数関数の特性である、`lim_(x>oo) x^n e^(x) = 0` が成り立つことから、計算結果は 0 となる。



一元一次方程式及其解 七上第三章一元一次方程式 發現學習的美麗新世界



Ex 一元一次不等式 定義及列式 國中數學七年級 下 發現學習的美麗新世界




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大师链




一次式の加法や減法 文字の前の数を足したり引くだけ 中学や高校の数学の計算問題




一次因式檢驗法 新版 Geogebra




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




幂级数连分式展开 多项式分式展开为幂级数的问题 三人行教育网 Www 3rxing Org



Priori Moe Gov Tw Download Textbook Math Grade7 Book2 Math 7 2 2 1 Pdf




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法




1 3多項式的乘除運算乙




中学1年生 数学 無料問題集 一次式の項をまとめる おかわりドリル




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download




一元一次方程 只含有一個未知數 即 元 並且未知數的最高次數為 華人百科




國中數學基礎講義 七下 八下 Shareclass



化簡二元一次式 二元一次聯立方程式 發現學習的美麗新世界
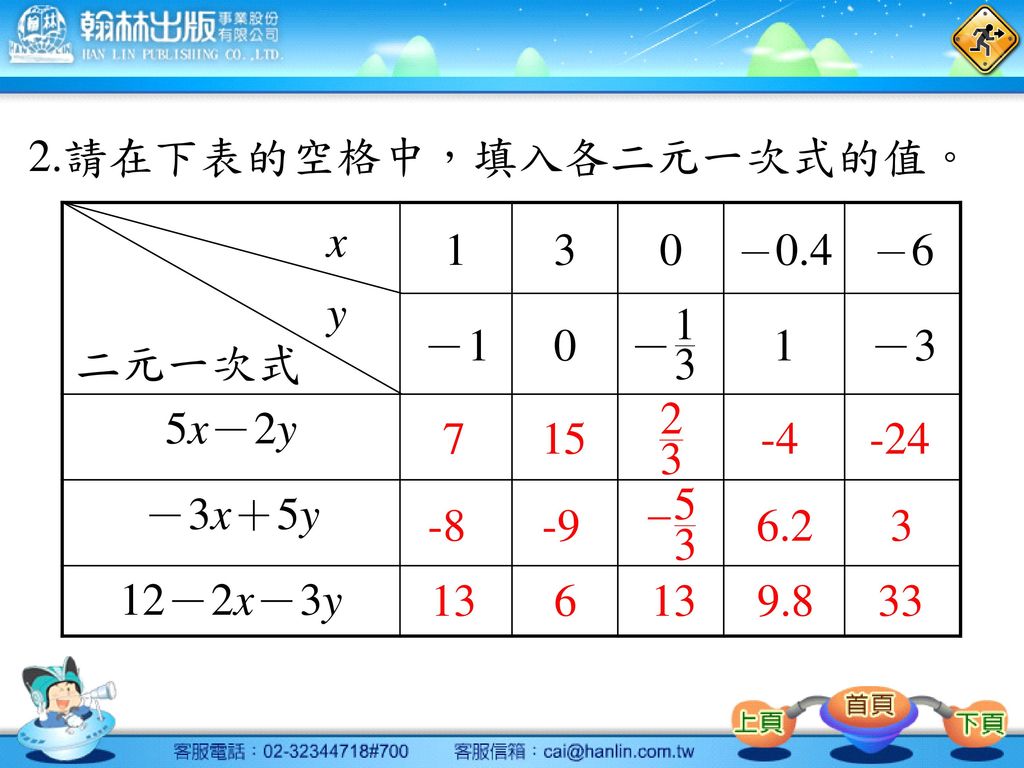



二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download



因式分解法解一元二次方程 禾教 初中数学互动课堂



数学1年



二元一次分式方程讲解 西瓜视频搜索




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
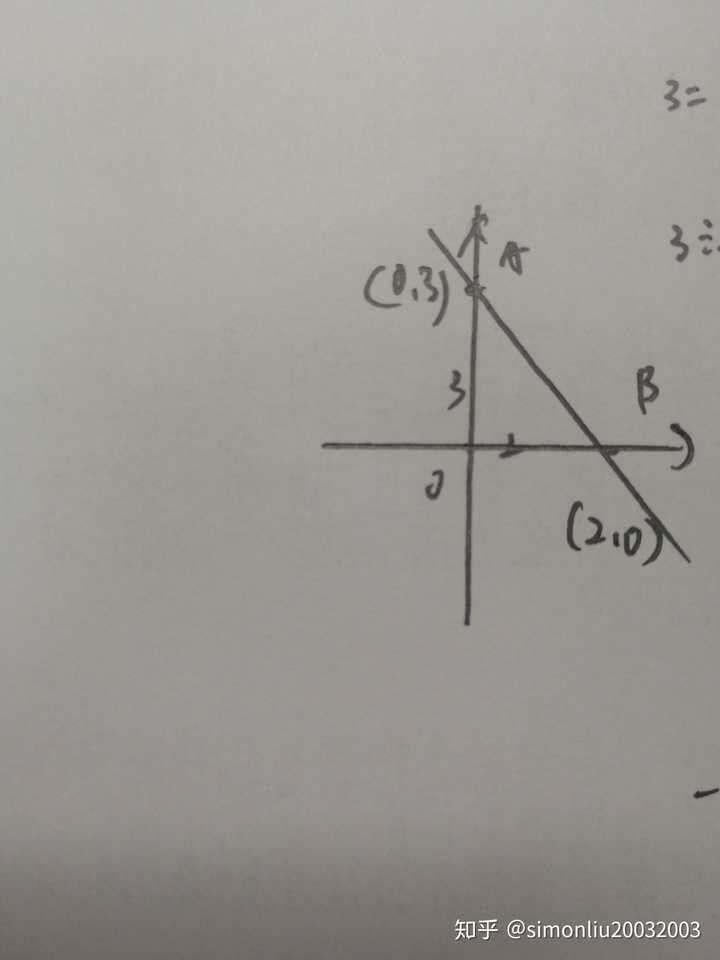



一次函数解析式的确定 一次函数五种表达式 一次函数的四种解析式




藍海學習計畫 國一 一元一次式mindmapping




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




この式は一次式ですか それとも一次式ではありませんか Clear




快乐数学 圆锥曲线之同构式行列式解二元一次方程组平面法向量速求 哔哩哔哩




Ppt 4 1 因式分解解一元二次方程式powerpoint Presentation Id



Http Www3 Nccu Edu Tw G Essh Industry Work 2 1 6 Pdf




2 で X Yの一次式の積となるための条件はd Clear




翻轉學習影片 國中 數學 4 1 1 二元一次式的意義 值與化簡




中学1年数学 一次式の文字の項と数字の項の記述の順番を徹底調査 Sprouts Diary In Nz




二元一次式的化簡綜合應用 Youtube




一元一次式和一元一次方程式哪裡不一樣 Youtube




新泰國中停課不停學七下第二章二元一次聯立方程式心智圖預習單 Shareclass



U9j580gf8iba369ji2w Xyz P 377




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア
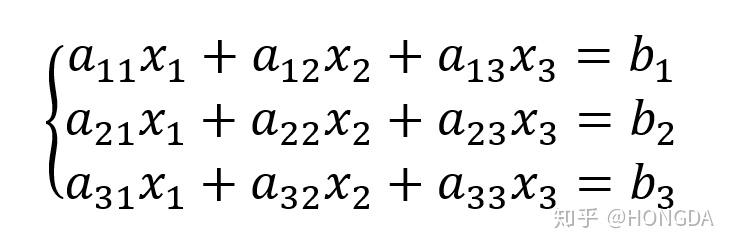



关于线性代数三阶行列式运算法则的推导 二 知乎



Www Camdemy Com Sysdata Users 1 1 Folder Fafd3d33cae Attach F9a3b02e41ae28ada250ea3353ea4a Pdf




國一國中數學的一元一次方程式筆記 Clear




一元一次式代數式化簡 Shareclass




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大师链



代數之一元一次式 Live 多媒體數學觀念典online




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




七年级数学第八章丨二元一次方程组 框架图 例题




初中數學 解二元一次方程組 哪些步驟容易錯 每日頭條
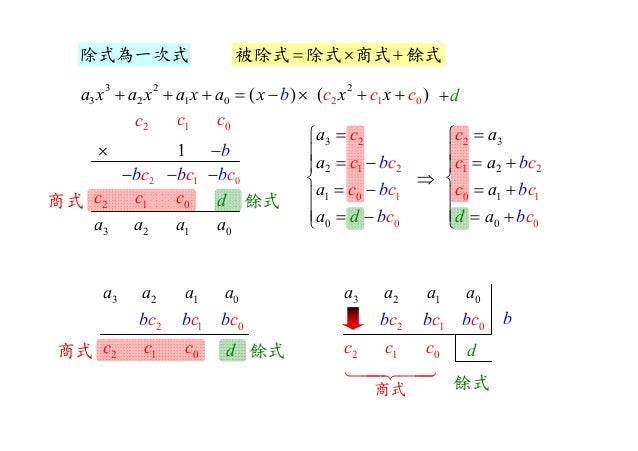



綜合除法




8 解一元一次方程式 下列哪一個步驟開始發生錯誤 A 步驟 阿摩線上測驗



Www Boyo Org Tw Boyo Index Php Downloads Category 25 17 10 16 09 09 14 Download 703 Pdf
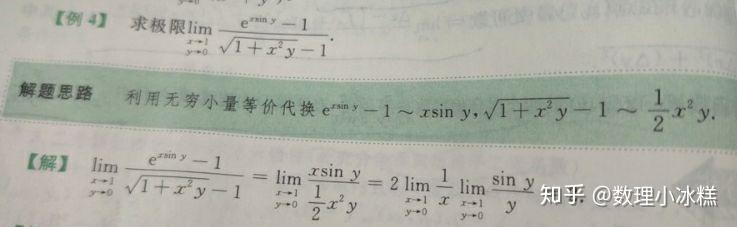



数学三 多元函数微分学 计算篇1 知乎




二元二次式可分解為一次式相乘的充要條件 Isdp08am 隨意窩xuite日誌




觀念 一元一次方程式的意義 數學 均一教育平台




人教版数学 七年级下册第八章 消元 解二元一次方程组 三好网




109 國中數學1 下補充資料 Shareclass



综合除法 万图壁纸网




基礎 一元一次式的化簡 除法與分配律 Youtube




陳擎文教學網 Python求解數學式 高中數學 大學數學 工程數學數學 微積分




109 國中數學1 下補充資料 Shareclass




この問題でルートの中を完全方程式にするっていうのは問題文で言ってる 高校 教えて Goo




多项式的计算与因式分解 哔哩哔哩



一次函数y与x的关系式 西瓜视频搜索



一次函数y与x的关系式 西瓜视频搜索



数学1年



5 一元一次方程式on Vimeo




二元一次式的化簡例1 例4 Youtube




翻轉學習影片 國中 數學 一元一次方程式 式子的值




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




康軒國中數學影音頻道 知識概念影片 7下




一元二次方程求根公式




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




國中數學總複習 5 一元一次方程式 莫博士 帶你長知識 大师链



精實數學主教材 7級



Q A 二次対策 X 2 2y 2 Xy Kx 2y 4 が X Yについての1次式の積に分解される時 Kの値は なぜ2回判別式 ブログやる気先生の 逆転の数学




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




二元一次方程组的解法 知乎




康軒國中數學影音頻道 知識概念影片 7下




一般 解一元一次方程式 等式兩邊未知數的比較 已下架內容 均一教育平台




Uidemy 雲端學堂 2 2一次因式檢驗法




待定系数法求一次函数的解析式练习题 Doc 三九文库网




國中數學的一元一次方程式筆記 Clear
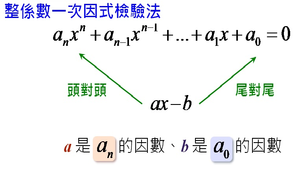



一次因式檢驗法的應用



名師課輔網 二元一次式圖形 第8題




多项式综合除法简化运算 知乎




翻轉學習影片 國中 數學 什麼是一元一次式




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




國中數學總複習 6 二元一次聯立方程式 莫博士 帶你長知識 大师链




一般 一元一次式的化簡 分數型1 Youtube



0 件のコメント:
コメントを投稿